Mireille Bousquet-Mélou

Une chercheuse à la croisée des chemins
Mireille Bousquet-Mélou est directrice de recherche CNRS au Laboratoire Bordelais de Recherche en Informatique (LaBRI), le laboratoire d’informatique de l’Université de Bordeaux. Cette année, elle a été récompensée de la Médaille d’argent du CNRS. Portrait d’une chercheuse dont les travaux se situent entre les mathématiques et l’informatique…
Spécialiste de combinatoire énumérative
Le domaine de recherche de Mireille Bousquet-Mélou se nomme la combinatoire énumérative. Concrètement, cela consiste à compter, à dénombrer, à trouver les formules qui décrivent le nombre de ceci ou de cela. Par exemple, une formule bien connue est celle des coefficients binomiaux Cnk, qui donne le nombre de manières de choisir k éléments parmi n.
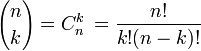
La combinatoire énumérative possède des interactions à la fois avec l’informatique, en particulier l’analyse de l’efficacité des algorithmes, et avec différents domaines des mathématiques, comme par exemple l’algèbre, notamment la représentation des groupes classiques, ou encore les probabilités discrètes. « C’est ce qui me plaît dans ce domaine de recherche : la variété des outils utilisés, des domaines d’interaction », s’enthousiasme Mireille Bousquet-Mélou. « C’est un domaine qui fait feu de tout bois ! »
Des chemins sur une grille carrée
Prenons une grille carrée sur laquelle on peut « marcher » dans n’importe quelle direction (haut, bas, droite ou gauche) en suivant les lignes. Un exemple de problème de combinatoire énumérative consiste à se demander combien de chemins ne se recoupant pas et ayant un nombre de pas fixé n on peut y tracer.
Pour n = 1 il y a 4 chemins possibles.
Pour n = 2, il y en a 12.
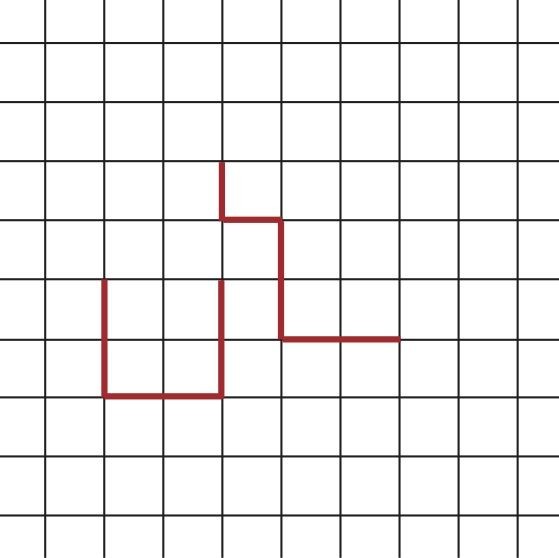
Deux chemins pour n = 6
« On ne connaît pas de formule générale donnant le nombre de chemins pour tout n », nous apprend Mireille Bousquet-Mélou avant de préciser que « si une telle formule existe, elle n’est probablement pas simple ».
Une autre question irrésolue depuis des décennies, qui intéresse les probabilistes, est la suivante : si on prend un chemin de longueur n au hasard, quand n est grand, à quelle distance le point d’arrivée se trouve-t-il du point de départ ?
« Ces problèmes possèdent aussi des liens avec la physique statistique », ajoute-t-elle. « Les chemins en question peuvent être pensés comme des polymères. »
Pour sa part, elle travaille notamment sur des questions similaires : « Des chemins auto-évitants, mais aussi des problèmes de chemins en 2D ou 3D, qui peuvent se couper mais sont contraints à rester dans une portion de l’espace. Ce sont des problèmes de dénombrement mais qui comportent aussi un peu de calcul formel. »
La vocation tranquille
De son enfance à Pau, Mireille Bousquet-Mélou se souvient avoir été « le modèle de la bonne élève », mais pas d’une vocation précoce pour les mathématiques : « J’avais de bonnes notes partout et aucune idée de ce que je voulais faire plus tard. » Elle s’oriente en classe préparatoire scientifique – qu’elle effectue à Toulouse – et intègre l’ENS, à Paris, à l’automne 1986. Elle y fait un DEA entre probabilités et statistiques, et découvre la combinatoire énumérative grâce à un cours « pétillant » de Xavier Viennot. Sous sa direction, elle commence par faire une thèse sur le dénombrement des polyominos.

Polyominos à 1, 2, 3, 4 ou 5 cases
« Quelques années après ma thèse », poursuit-elle, « j’ai eu la chance de tomber, grâce à un collègue, sur un très joli sujet qui concernait le dénombrement de certaines partitions d’entiers, avec des conditions originales sur les parts… L’occasion de trouver de belles formules. C’est un sujet qui a eu de la descendance. »
Au contact de Philippe Flajolet, qui a fédéré une communauté française de spécialistes de combinatoire, des probabilités, d’analyse d'algorithmes, elle s'intéresse aussi au dénombrement asymptotique.
Plusieurs séjours en Australie auprès de physiciens statisticiens lui donnent l’occasion de s’ouvrir à d’autres domaines, de formuler des questions autrement, d’explorer d’autres sujets : « C’est à ce moment-là que j'ai commencé à m'intéresser aux chemins auto-évitants. »
Dans sa discipline, les questions viennent souvent d’autres domaines des mathématiques : « Parfois, ces questions existent indépendamment dans plusieurs disciplines différentes. Par exemple, les chemins auto-évitants appartiennent autant à la combinatoire et aux probabilités qu’à la physique statistique. »
« Chatouiller le cerveau »
« Ce que j’aime dans la recherche en mathématiques », confie Mireille Bousquet-Mélou, « c’est que ce n’est jamais ennuyeux. Ça chatouille le cerveau. C’est prenant et stimulant. » Elle voit sa discipline comme « un jeu à très grande échelle », pour lequel il faut s’armer de persévérance, de ténacité et de patience : « On sèche la plupart du temps mais il y a aussi des moments où l’on sent que l’on est en train d’avancer, sans savoir où et comment. On entrevoit que l’on est sur le point de comprendre quelque chose. On est le siège d’une petite alchimie. C’est très intrigant. » Pour la chercheuse, la manière dont viennent les idées reste souvent un mystère : « Parfois, on découvre que la bonne façon de faire était en fait très simple. On se demande : mais pourquoi n’ai-je pas formulé ça de cette façon avant ? » Elle se souvient : « Il m’est déjà arrivé de me lever un matin en ayant enfin compris comment résoudre un point sur lequel je butais. C’est très curieux et ce caractère étrange a beaucoup de charme. »
Elle regrette que les mathématiques souffrent d’une image si effrayante : « En France, les mathématiques sont présentées comme le truc qu’il faut absolument savoir faire. Forcément, ça attire certaines personnes, mais ça en rebute beaucoup d’autres. Je crois qu’il faudrait laisser les gens s’approprier les maths, s’amuser avec. »
Les récompenses
Avant sa Médaille d’argent du CNRS, Mireille Bousquet-Mélou avait déjà été distinguée par la Médaille de bronze, ainsi que par un prix de l’Académie des Sciences en mathématiques. Ce qui n’a pas empêché sa surprise et son émotion à la réception de cette nouvelle récompense prestigieuse. « L’initiative émanait de l’INSMI – NDRL : l’institut de mathématiques du CNRS -, un institut qui n’est pas le mien puisque je travaille dans un laboratoire d’informatique », explique-t-elle, avant d’ajouter : « Être entre deux disciplines n’est pas toujours confortable, cela comporte certains attraits mais aussi quelques inconvénients. Cette récompense est une reconnaissance pour moi mais aussi pour mon domaine, qui est ainsi mis en lumière. »
Une distinction qui, peut-être, contribuera également à encourager des jeunes femmes sur la voie des mathématiques ou de l’informatique fondamentale. « C’est un constat de fait : il y a encore peu de femmes dans les mathématiques. L’informatique théorique n’est pas trop mal lotie en France, par rapport à d’autres pays (en 2012, en informatique, elles représentaient 23% des effectifs totaux des CR et DR du CNRS d'après les chiffres de l'INS2I, 26% des maîtres de conférence et 19% des professeurs). Ceci dit, je suis la seule femme de mon groupe, au LaBRI. » Et de conclure : « Je ne vois guère de changement pour l’avenir proche. Je crois que ce sont des évolutions qui viennent très lentement. »
Propos recueillis par Gaël Octavia en Juin 2014
When you subscribe to the blog, we will send you an e-mail when there are new updates on the site so you wouldn't miss them.


